Tunable Q-Factor Wavelet Transform (TQWT)
The TQWT is a constant-Q transform that is easily invertible, modestly oversampled, and satisfies Parseval's energy theorem.
Wavelet Transform with Tunable Q-Factor (635 KB, pdf file)
IEEE Trans. on Signal Processing. 59(8):3560-3575, August 2011.
I. W. Selesnick.
Download MATLAB software: tqwt_matlab_toolbox (1.7 MB, zip file)
version 1.7
Download software guide only: TQWT_guide (791 KB, pdf file)
Presentation slides (pdf)
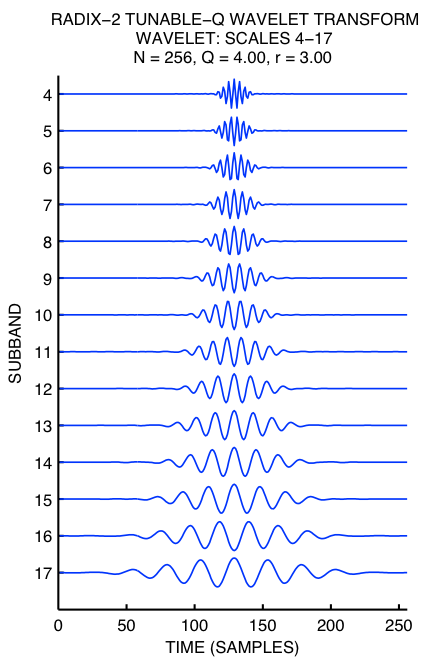
Abstract: This paper describes a discrete-time wavelet transform for which the Q-factor is easily specified. Hence, the transform can be tuned according to the oscillatory behavior of the signal to which it is applied. The transform is based on a real-valued scaling factor (dilation-factor) and is implemented using a perfect reconstruction over-sampled filter bank with real-valued sampling factors. Two forms of the transform are presented. The first form is defined for discrete-time signals defined on all of Z. The second form is defined for discrete-time signals of finite-length and can be implemented efficiently with FFTs. The transform is parameterized by its Q-factor and its oversampling rate (redundancy), with modest oversampling rates (e.g. 3-4 times overcomplete) being sufficient for the analysis/synthesis functions to be well localized.
This transform is similar to the rational-dilation wavelet transform (RADWT). An advantage of the TQWT in comparison with the RADWT is its faster implementation using radix-2 FFTs and the ease with which its Q-factor and redundancy can be tuned.
Acknowledgment
This material is based upon work supported by the National Science Foundation under Grant No. 1018020.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.