Rational-Dilation Wavelet Transforms (RADWT)
Also see the tunable Q-factor wavelet transform (TQWT).
Frequency-Domain Design of Overcomplete Rational-Dilation Wavelet Transforms (pdf file, 432 KB)
I. Bayram and I. W. Selesnick.
IEEE Trans. on Signal Processing.
57(8):2957-2972, August 2009.
MATLAB Software: radwt_toolbox_v2 (zip file, 969 KB)
Presentation slides: radwt_slides (pdf file, 1.3 MB)
Abstract: The dyadic wavelet transform is an effective tool for processing piecewise smooth signals; however, its poor frequency resolution (its low Q-factor) limits its effectiveness for processing oscillatory signals like speech, EEG, and vibration measurements, etc. This paper develops a more flexible family of wavelet transforms for which the frequency resolution can be varied. The new wavelet transform can attain higher Q-factors (desirable for processing oscillatory signals) or the same low Q-factor of the dyadic wavelet transform. The new wavelet transform is modestly overcomplete and based on rational dilations. Like the dyadic wavelet transform, it is an easily invertible 'constant-Q' discrete transform implemented using iterated filter banks and can likewise be associated with a wavelet frame for L2(R). The wavelet can be made to resemble a Gabor function and can hence have good concentration in the time-frequency plane. The construction of the new wavelet transform depends on the judicious use of both the transform's redundancy and the flexibility allowed by frequency-domain filter design.
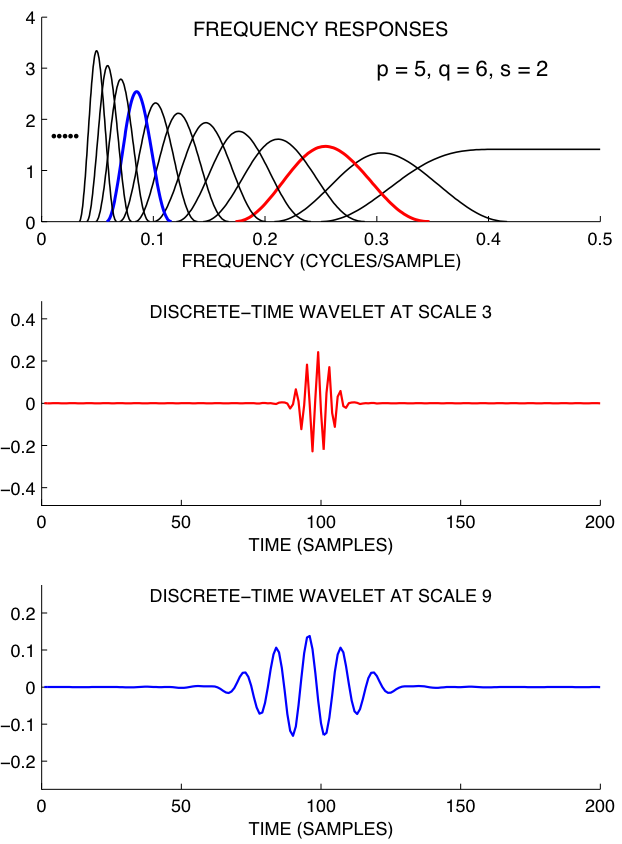
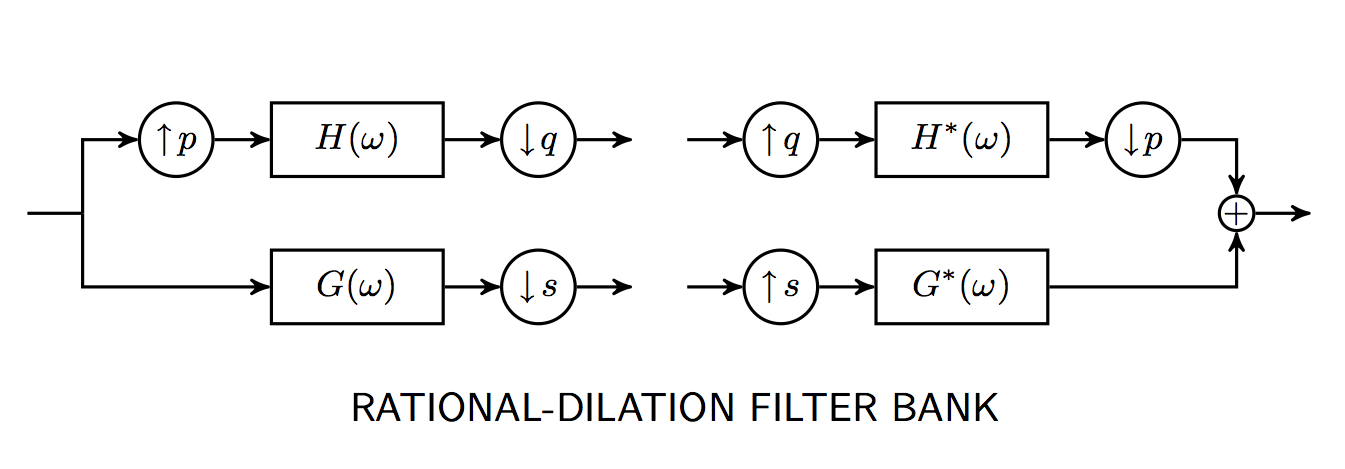
Overcomplete Discrete Wavelet Transforms with Rational Dilation Factors (pdf file, 552 KB)
I. Bayram and I. W. Selesnick.
IEEE Trans. on Signal Processing.
57(1):131-145, January 2009.
Preprint (pdf file, 1.7 MB)
Abstract: This paper develops an overcomplete discrete wavelet transform (DWT) based on rational scaling factors. The proposed overcomplete rational DWT is implemented using self-inverting FIR filter banks, is approximately shift-invariant, and can provide a dense sampling of the time-frequency plane. A straightforward algorithm is described for the construction of minimal-length perfect reconstruction filters with a specified number of vanishing moments; whereas, in the non-redundant rational case, no such algorithm is available. The algorithm is based on matrix spectral factorization. The analysis/synthesis functions (discrete-time wavelets) can be very smooth and can be designed to closely approximate the derivatives of the Gaussian function.
Design of Orthonormal and Overcomplete Wavelet Transforms Based on Rational Sampling Factors (pdf file, 652 KB)
I. Bayram and I. W. Selesnick.
In Wavelet Applications in Industrial Processing V, Proceedings of
SPIE, volume 6763, September 11-12, 2007.
Abstract: Most wavelet transforms used in practice are based on integer sampling factors. Wavelet transforms based on rational sampling factors offer in principle the potential for time-scale signal representations having a finer frequency resolution. Previous work on rational wavelet transforms and filter banks includes filter design methods and frequency domain implementations. We present several specific examples of Daubechies-type filters for a discrete orthonormal rational wavelet transform (FIR filters having a maximum number of vanishing moments) obtained using Grobner bases. We also present the design of overcomplete rational wavelet transforms (tight frames) with FIR filters obtained using polynomial matrix spectral factorization.