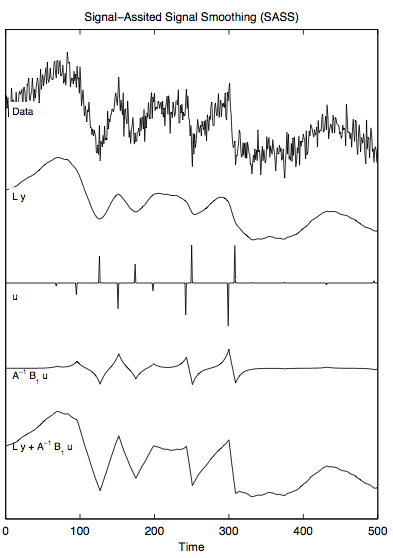
Abstract: This chapter describes a method for one-dimensional signal denoising that simultaneously utilizes both conventional linear time-invariant (LTI) filtering principles and sparse optimization principles. The method, called 'sparsity-assisted signal smoothing' (SASS), is based on modeling a signal as the sum of a low-pass component and a piecewise smooth component. The problem is formulated as a sparse-regularized linear inverse problem. We provide simple direct methods to set the regularization parameter and the non-convexity parameter, the later if a non-convex penalty is utilized. We derive an iterative optimization algorithm that harnesses the computational efficiency of fast solvers for banded systems. The SASS approach performs a type of wavelet denoising, but does so through sparse optimization rather than through wavelet transforms. The approach is relatively free of the pseudo-Gibbs phenomena that tends to arise in wavelet denoising.
Sparsity-Assisted Signal Smoothing (Revisited) [ICASSP, March 2017]
slides [ICASSP, March 2017]
Sparsity-Assisted Signal Smoothing [Excursions in Harmonic Analysis, Vol 4. Birkhauser, 2015]
SASS_software_ver3 (folder)
SASS_software_ver3.zip (zip file)
SASS_toolbox.zip (zip file)

Ivan W. Selesnick
Dept of Electrical and Computer Engineering
NYU Polytechnic School of Engineering
Brooklyn, NY 11201
This material is based upon work supported by the National Science Foundation under Grant No. 1018020.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.