Example 1: 1D group-sparse signal denoising using overlapping group shrinkage (OGS)

Illustrate overlapping group shrinkage (OGS) for denoising a signal with group sparsity property. OGS takes into account the group sparsity property of the signal.

Po-Yu Chen and Ivan Selesnick
Polytechnic Institute of New York University
New York, USA
March 2012

Contents

Start

clear
% close all
randn('state', 0);               % Initialize state so as to exactly reproduce the example

printme = @(txt) print('-dpdf', sprintf('figures/Example1_%s', txt));

Create signal

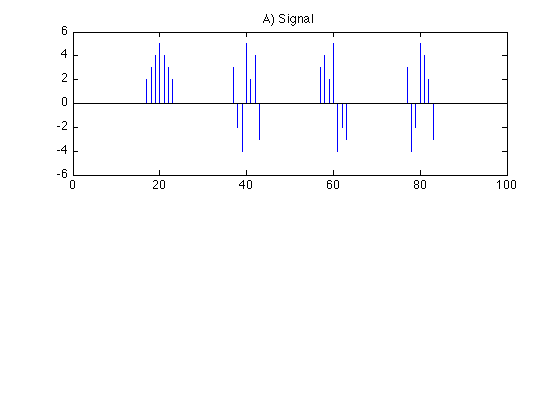
Create signal with group sparsity property.

N = 100;                                % N : length of signal
x = zeros(N, 1);                        % x : signal (with no noise)
x(20+(-3:3)) = [2 3 4 5 4 3 2];
x(40+(-3:3)) = [3 -2 -4 5 2 4 -3];
x(60+(-3:3)) = [3 4 2 5 -4 -2 -3];
x(80+(-3:3)) = [3 -4 -2 5 4 2 -3];

figure(1)
clf
subplot(2, 1, 1)
stem(x, 'marker', 'none')
title('A) Signal')
M = 6;
ylim1 = [-M M];
ylim(ylim1)

Create noisy signal

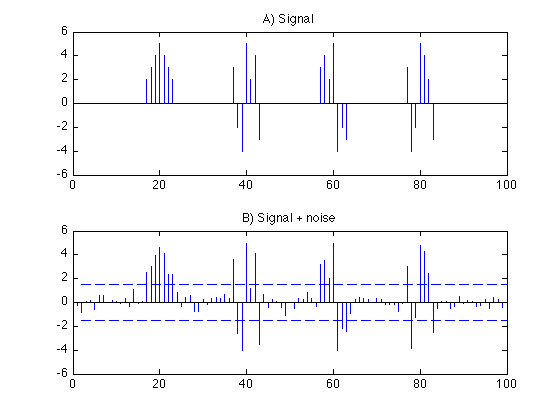
The red line shows A*sigma. Most of the noise is within this margin. This can be considered the 'noise envelope'.

sigma = 0.5;                        % sigma : standard deviation of noise

y = x + sigma .* randn(N, 1);       % y : signal + noise

A = 3;                              % A : multiplier to define noise envelope

figure(1)
subplot(2, 1, 2)
stem(y, 'marker', 'none')
line([1 N], A*sigma*[1 1], 'linestyle', '--')
line([1 N], -A*sigma*[1 1], 'linestyle', '--')
title('B) Signal + noise')
ylim(ylim1)
printme('data')

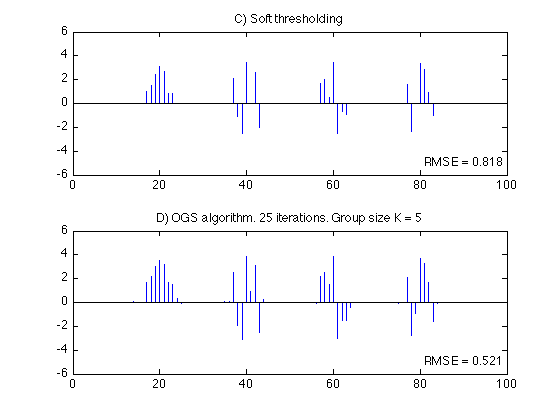
Soft-thresholding

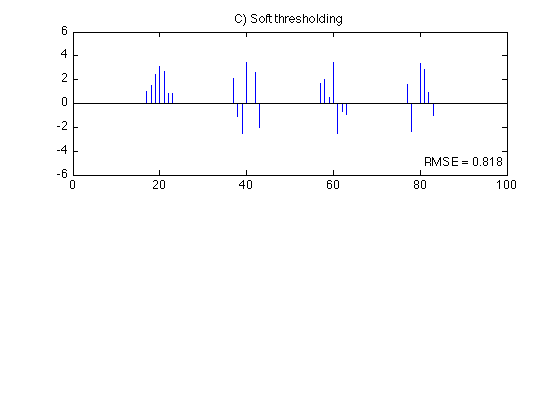
Denoise the signal using the soft thresholding rule. Setting the threshold to A*sigma removes near all the noise.

T = A * sigma;                      % T : threshold
x1 = soft(y, T);                    % apply soft thresholding
rmse = sqrt(mean((x-x1).^2));       % rmse : root mean square error

figure(2)
clf
subplot(2, 1, 1)
stem(x1, 'marker', 'none')
title('C) Soft thresholding')
ylim(ylim1)
txt = sprintf('RMSE = %.3f', rmse);
axnote(txt)

Note that soft thresholding applied to white standard normal (zero-mean, unit variance) noise leads to an output std of about 0.02.

yy = randn(1, 10000000);
xx = soft(yy, 3);
std(xx(:))      % gives  0.02

ans =

    0.0203

So, for OGS, we will set lambda to a value that leads to the same output std of 0.02 when OGS is applied to standard normal white noise.

Overlapping group shrinkage (OGS)

Denoise the signal using the overlapping group shrinkage (OGS) algorithm. This is an iterative algorithm.

Nit = 25;                       % Nit : number of iterations
K = 5;                          % K : group size parameter
lambda = 0.68 * sigma;          % lambda: regularization parameter for OGS

[x2, cost] = ogshrink(y, K, lambda, Nit);       % Run the OGS algorithm
rmse = sqrt(mean((x-x2).^2));                   % rmse : root mean square error

figure(2)
subplot(2, 1, 2)
stem(x2, 'marker', 'none')
txt = sprintf('D) OGS algorithm. %d iterations. Group size K = %d', Nit, K);
title(txt)
ylim(ylim1)
txt = sprintf('RMSE = %.3f', rmse);
axnote(txt)

printme('denoised')

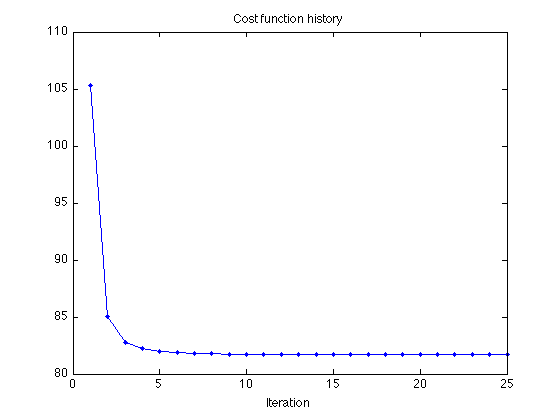
Display cost function history of OGS algorithm

figure(3)
clf
plot(1:Nit, cost, '.-') % , 'markersize', 16)
title('Cost function history')
xlabel('Iteration')
printme('cost')

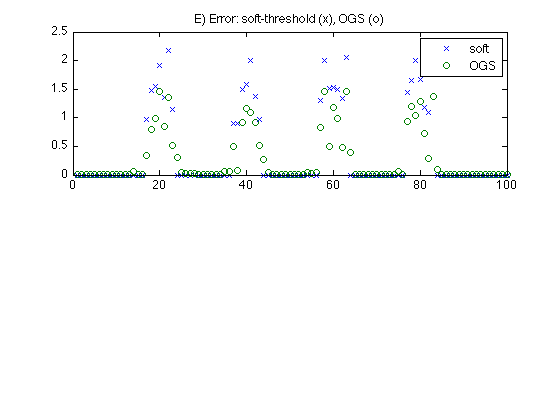
Comparison: Soft thresholding and OGS

err1 = abs(x - x1);
err2 = abs(x - x2);

figure(1)
clf
subplot(2,1,1)
plot(1:N, err1, 'x', 1:N, err2, 'o')
legend('soft', 'OGS')
title('E) Error: soft-threshold (x), OGS (o)');
printme('compare')

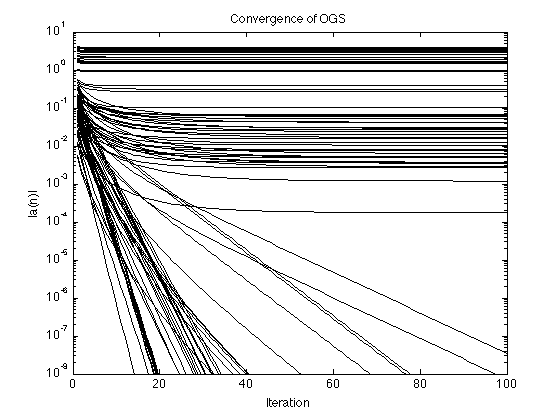
Convergence of OGS

Here is the OGS algorithm with all intermediate solutions stored in a matrix A, so that the convergence of the solution can be subsequently visualized.

% function [a, cost] = ogshrink(y, K, lam, Nit)
% y   : 1-D  noisy signal (vector)
% K   : size of group
% lam : regularization parameter
% Nit : number of iterations

lam = lambda;
Nit = 100;

N = length(y);
A = zeros(N, Nit);

a = y(:);                  % initialize
h = ones(1, K);           % for convolution
cost = zeros(1, Nit);
for it = 1:Nit
    r = sqrt(conv(abs(a).^2, h));
    cost(it) = 0.5*sum(abs(y - a).^2) + lam * sum(r);
    v = 1 + lam*conv(1./r, h);
    v = v(K:end+1-K);
    a = y./v;
    A(:, it) = a;
end


figure(1)
clf
semilogy(abs(A'), 'black')
title('Convergence of OGS')
ylim([1e-8 10]);
xlabel('Iteration')
ylabel('|a(n)|')

printme('convergence')

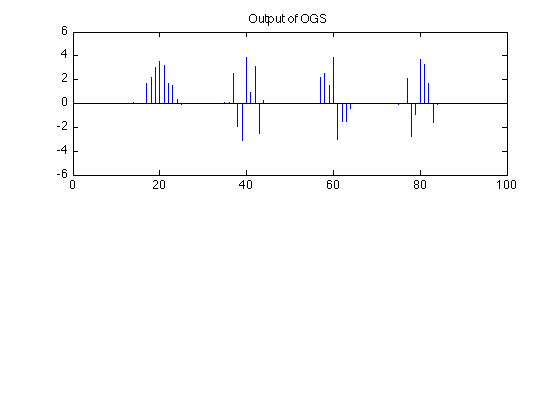
figure(2)
clf
subplot(2, 1, 1)
stem(a, 'marker', 'none')
ylim(ylim1)
title('Output of OGS')

Published with MATLAB® 7.8