Example: Sparse deconvolution
Deconvolution of a spike signal with a comparison of two penalty functions. The algorithm is based on quadratic MM and uses a fast solver for banded systems.
Reference: Penalty and Shrinkage Functions for Sparse Signal Processing Ivan Selesnick, NYU-Poly, selesi@poly.edu, 2012
http://eeweb.poly.edu/iselesni/lecture_notes/
Contents
Start
close all clear randn('state',0); % set state so that example can be reproduced printme = @(txt) print('-dpdf', sprintf('figures/Example_%s',txt));
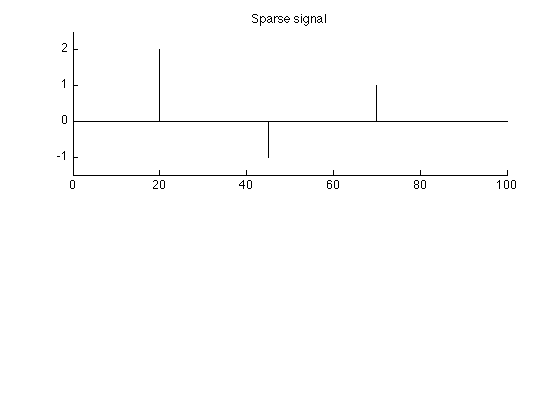
Create spike signal
N = 100; % N : length of signal s = zeros(N,1); k = [20 45 70]; a = [2 -1 1]; % a : spike amplitudes s(k) = a; % s : spike signal figure(1) clf subplot(2,1,1) stem(s, 'marker', 'none') box off title('Sparse signal'); ylim1 = [-1.5 2.5]; ylim(ylim1) printme('original')
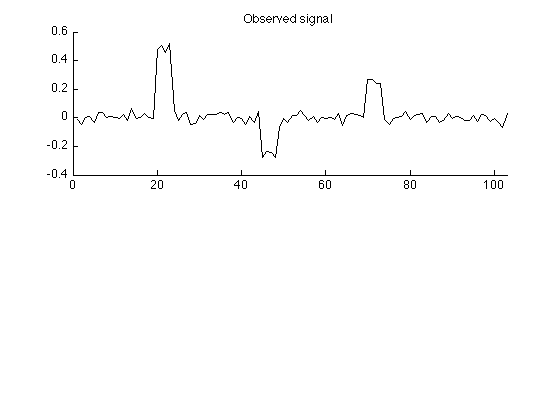
Create observed signal
The simulated observed signal is obtained by convolving the signal with a 4-point impulse response and adding noise.
L = 4; % L : length of impulse response h = ones(L,1)/L; % h : impulse response M = N + L - 1; % M : length of observed signal sigma = 0.03; % sigma : standard deviation of AWGN w = sigma * randn(M,1); % w : additive zero-mean Gaussian noise (AWGN) y = conv(h,s) + w; % y : observed data figure(2) clf subplot(2,1,1) plot(y) box off xlim([0 M]) title('Observed signal'); printme('observed')
Create convolution matrix H
Create the convolution matrix H using Matlab sparse matrix functions 'sparse' and 'spdiags'. By making H a sparse matrix: - less memory is used, - multiplying vectors by H is faster, - fast algorithms for solving banded systems will be used.
H = sparse(M,N); e = ones(N,1); for i = 0:L-1 H = H + spdiags(h(i+1)*e, -i, M, N); % H : convolution matrix (sparse) end issparse(H) % confirm that H is a sparse matrix
ans =
1
Verify that H*s is the same as conv(h,s)
err = H*s - conv(h,s);
max_err = max(abs(err));
fprintf('Maximum error = %g\n', max_err)
Maximum error = 0
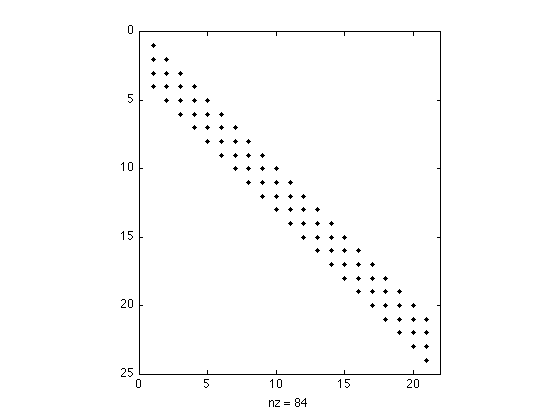
Display structure of convolution matrix. Note that the matrix is banded (sparse).
figure(1) clf spy(H(1:24,1:21))
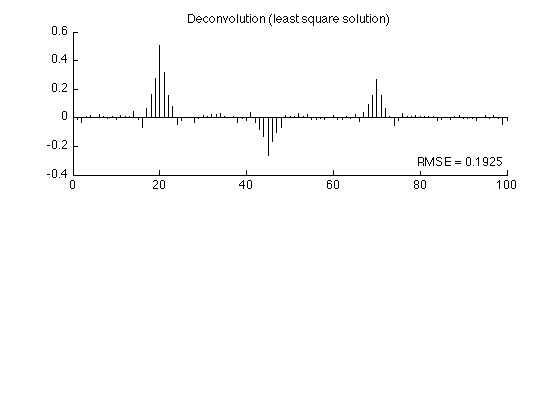
Least square solution
Find the least square solution to the deconvolution problem.
lambda = 0.4; % lambda : regularization parameter x_L2 = (H'*H + lambda*speye(N)) \ (H' * y); % x_L2 : least square solution rmse_L2 = sqrt(mean((x_L2 - s).^2)); fprintf('Least square solution: RMSE = %f\n', rmse_L2); figure(2) clf subplot(2,1,1) stem(x_L2, 'marker', 'none') box off title('Deconvolution (least square solution)'); axnote(sprintf('RMSE = %.4f', rmse_L2)) printme('L2')
Least square solution: RMSE = 0.192453
Verify banded system solver
Verify that MATLAB calls LAPACKS's fast algorithm for solving banded systems
spparms('spumoni', 3); % Set sparse monitor flag to obtain diagnostic output x_L2 = (H'*H + lambda*speye(N)) \ (H' * y); % x_L2 : least square solution % Diagnostic output: % % sp\: bandwidth = 3+1+3. % sp\: is A diagonal? no. % sp\: is band density (1.00) > bandden (0.50) to try banded solver? yes. % sp\: is LAPACK's banded solver successful? yes. spparms('spumoni', 0); % Reset sparse monitor flag to no diagnostic output
sp\: bandwidth = 3+1+3. sp\: is A diagonal? no. sp\: is band density (1.00) > bandden (0.50) to try banded solver? yes. sp\: is LAPACK's banded solver successful? yes.
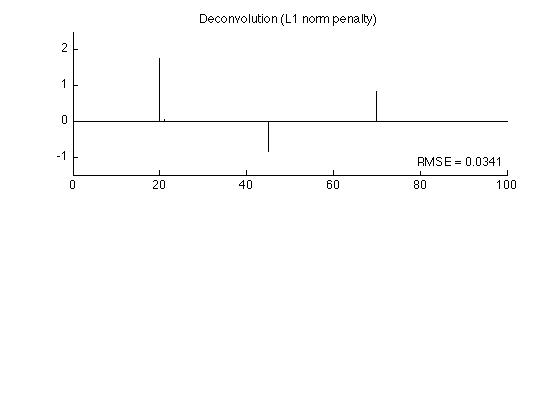
Sparse deconvolution - L1 norm penalty
The penalty function is phi(x) = lam abs(x)
T = 3 * sigma * sqrt(sum(abs(h).^2)); % T : threshold using '3-sigma' rule lam = T; Nit = 50; phi_L1 = @(x) lam * abs(x); wfun_L1 = @(x) abs(x)/lam; dphi_L1 = @(x) lam * sign(x); [x1, cost1] = deconv_MM(y, phi_L1, wfun_L1, H, Nit); rmse1 = sqrt(mean((x1 - s).^2)); fprintf('L1 norm solution: RMSE = %f\n', rmse1);
L1 norm solution: RMSE = 0.034072
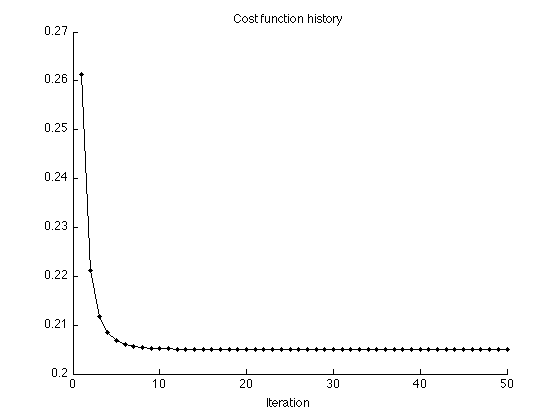
Display cost function history
figure(1) clf plot(1:Nit, cost1, '.-') title('Cost function history'); xlabel('Iteration') xlim([0 Nit]) box off printme('CostFunction_L1')
The L1 solution is quite similar to the original signal (much more so than the least square solution).
figure(2) clf subplot(2,1,1) stem(x1, 'marker', 'none') box off ylim(ylim1); title('Deconvolution (L1 norm penalty)'); axnote(sprintf('RMSE = %.4f', rmse1)) printme('L1')
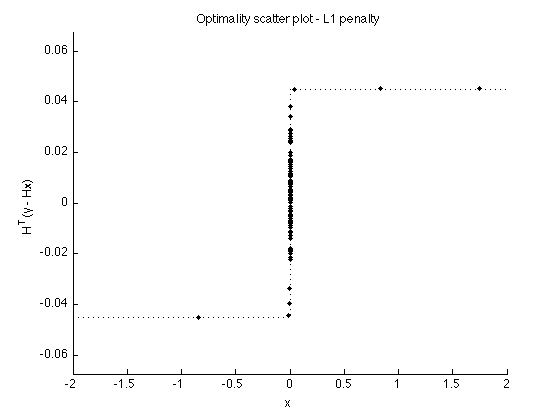
Verify optimality conditions
v1 = H'*(y-H*x1); t = [linspace(-2, -eps, 100) linspace(eps, 2, 100)]; figure(1) clf plot(x1, v1, '.') line(t, dphi_L1(t), 'linestyle', ':') box off ylim([-1 1]*lam*1.5) xlabel('x') ylabel('H^T(y - Hx)') title('Optimality scatter plot - L1 penalty'); printme('scatter_L1')
Sparse deconvolution - nn garrote penalty
The penalty function corresponds to the nn garrote shrinkage function.
dphi = @(x) 0.5 * (- abs(x) + sqrt( x.^2 + 4*T^2 ) ) .* sign(x); phi = @(x) T^2*asinh(abs(x)/(2*T)) +0.25 * (abs(x).*sqrt(4*T^2+x.^2)-x.^2) ; wfun = @(x) 1/(2*T^2) * abs(x) .* ( sqrt(x.^2 + 4*T^2) + abs(x) ); % x / dphi(x) [x2, cost2] = deconv_MM(y, phi, wfun, H, Nit); rmse2 = sqrt(mean((x2 - s).^2)); fprintf('nn-garrote solution: RMSE = %f\n', rmse2);
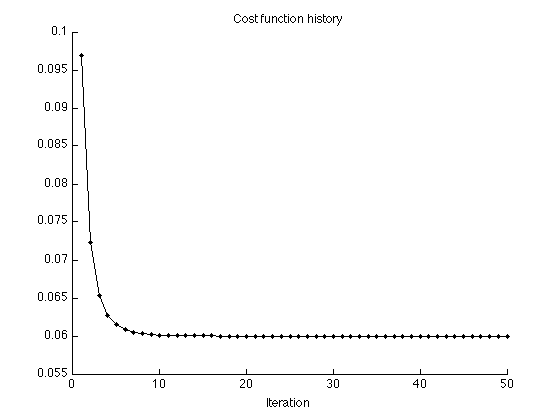
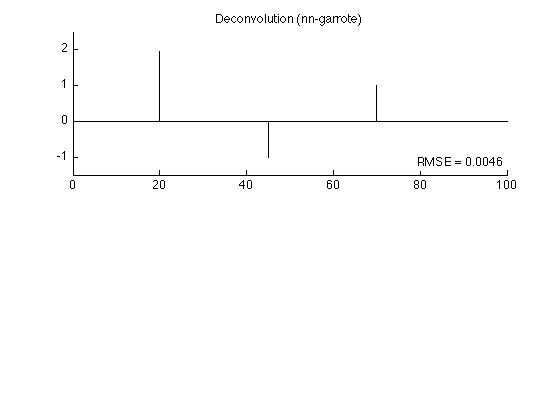
nn-garrote solution: RMSE = 0.004564
Display cost function history
figure(1) clf plot(1:Nit, cost2, '.-') title('Cost function history'); xlabel('Iteration') xlim([0 Nit]) box off printme('CostFunction_garrote')
figure(2) clf subplot(2,1,1) stem(x2, 'marker', 'none') box off ylim(ylim1); title('Deconvolution (nn-garrote)'); axnote(sprintf('RMSE = %.4f', rmse2)) printme('garrote')
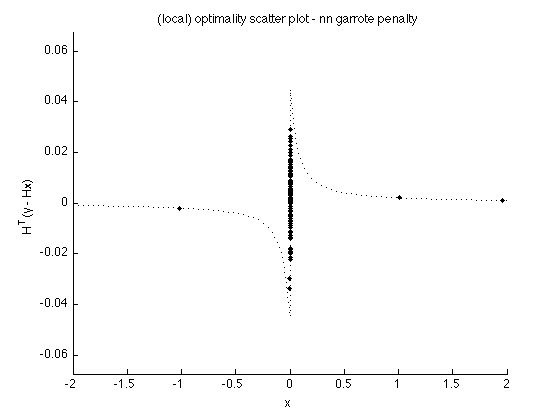
Verify (local) optimality conditions
v2 = H'*(y-H*x2); figure(1) clf plot(x2, v2, '.') line(t, dphi(t), 'linestyle', ':') box off ylim([-1 1]*T*1.5) xlim(t([1 end])) xlabel('x') ylabel('H^T(y - Hx)') title('(local) optimality scatter plot - nn garrote penalty'); printme('scatter_garrote')
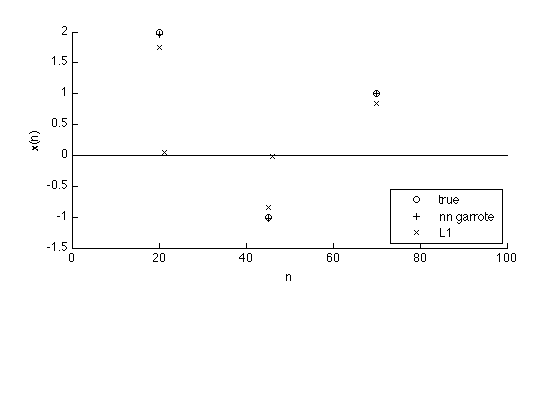
Comparison
The nn garrote penalty is more accurate than the L1 norm penalty. The result obtained using the L1 norm penalty is attenuated compared with the true signal.
n = 1:N; k = abs(s) > 1e-5; k1 = abs(x1) > 1e-5; k2 = abs(x2) > 1e-5; figure(1) clf subplot(3,1,[1 2]) plot(n(k), s(k), 'o') hold on plot(n(k2), x2(k2),'+', n(k1), x1(k1),'x') line([0 N], [0 0]) hold off xlim([0 N]) legend('true', 'nn garrote', 'L1', 'location', 'se') box off xlabel('n') ylabel('x(n)') printme('compare')