Image Denoising
1. Matlab Implementation
One technique for denoising is wavelet thresholding (or "shrinkage"). When we decompose data using the wavelet transform, we use filters that act as averaging filters, and others that produce details. Some of the resulting wavelet coefficients correspond to details in the data set (high frequency sub-bands). If the details are small, they might be omitted without substantially affecting the main features of the data set. The idea of thresholding is to set all high frequency sub-band coefficients that are less than a particular threshold to zero. These coefficients are used in an inverse wavelet transformation to reconstruct the data set [2].
After implementing the separable DWT, real Dual-Tree DWT, complex Dual-Tree DWT for 1-D, 2-D and 3-D signal, we can use three different methods to remove the noise from an image. These methods are using separable 2-D DWT (code: denS2D.m), real 2-D dual-tree DWT (code: denR2D.m), and complex 2-D dual-tree DWT(code: denC2D.m). In this section, these methods will be introduced and comparison will also be made. Separable 2-D DWT method is first introduced in table 7.1.
Table 7.1 Matlab function denS2D.m
function y = denS2D(x,T)
% x: noise signal
% T: threshold
[af, sf] = farras;
J = 4;
w = dwt2D(x,J,af);
% loop thru scales:
for j = 1:J
% loop thru subbands
for s = 1:3
w{j}{s} = soft(w{j}{s},T);
end
end
y = idwt2D(w,J,sf);
This program has two parameters, one for noise signal and the other for threshold point. A sample noise signal is shown below, whose dimension is 512 x 512. We first take the forward DWT over 4 scales (J=4). Then a denoising method called soft thresholding is applied to wavelet coefficients through all scales and subbands. Function soft sets coefficients with values less than the threshold(T) to 0, then substracts T from the non-zero coefficients. After soft thresholding, we take inverse wavelet transform.

The following example shows how to convert an image to double data type, how to creat a noise signal and display the denoised image. Note that we use a threshold value of 35, which is the optimal threshold point for this case. We will introduce how to find the optimal threshold value in the later part of this section.
EXAMPLE (NOISE REMOVAL)>> s1 = double(imread('st.tif'));
>> s = s1(:,:,3);
>> x = s + 20*randn(size(s));
>> T = 35;
>> y = denS2D(x,T);
>> imagesc(y)
>> colormap(gray)
>> axis image
|
From the resulting image, we can see the denoising capability of separable 2-D DWT. Click on the image to see the true size. Now we want to improve the effect by using complex 2-D dual-tree DWT. The optimal threshold value for this method is 40. Matlab function denC2D.m and the denoised image are shown below.
Table 7.2 Matlab function denC2D.m
function y = denC2D(x,T);
[Faf, Fsf] = FSfarras;
[af, sf] = dualfilt1;
J = 4;
w = cplxdual2D(x,J,Faf,af);
I = sqrt(-1);
% loop thru scales:
for j = 1:J
% loop thru subbands
for s1 = 1:2
for s2 = 1:3
C = w{j}{1}{s1}{s2} + I*w{j}{2}{s1}{s2};
C = soft(C,T);
w{j}{1}{s1}{s2} = real(C);
w{j}{2}{s1}{s2} = imag(C);
end
end
end
y = icplxdual2D(w,J,Fsf,sf);
The difference between the above two denoised images is subtle. We can enlarge the figures and focuse on a small area of these figures to see the difference. The following figures are produced by function den3.m.
|
Enlarged image 1 |
|
Enlarged image 2 |
We can see that complex 2-D dual-tree method removes more noise signal than separable 2-D method does. Actually, 2-D dual-tree method outperforms separable method. This can be proved by the "rms error V.S. threshold points" plot, which is shown below.
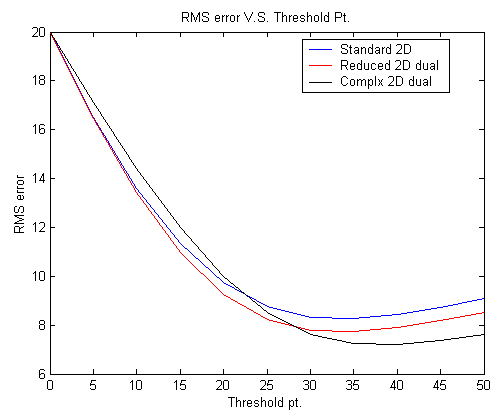
It illustrates the denoising capability for three different methods with complex 2-D dual-tree method be the best, followed by real 2-D dual-tree method and separable method. Also, it tells us where the optimal threshold points locate. For each method, applying the optimal threshold point yields the mininum RMS error. Therefore, a threshold producing the minimum RMS error is the optimal one. A part of function den3.m generate this figure.
A PART OF FUNCTION den3.ms1 = double(imread('st.tif'));
s = s1(:,:,3);
x = s + 20*randn(size(s));
t = 0:5:50; % threshold range(0~50),increment by 5
e = den2(s,x,t); % using separable method
re = rden2(s,x,t); % using real 2-D dual-tree method
ce = cden2(s,x,t); % using complex 2-D dual-tree method
|
We should note that plotting rms error requires one more parameter, which is the original image. Therefore, function den2.m, rden2.m and cden2.m are used.
Summary of programs:
- denS2D.m - Denoising by using separable 2-D DWT
- denR2D.m - Using 2-D dual-tree DWT (real)
- denC2D.m - Using complex 2-D dual-tree DWT
- den2.m - Compute rms error for separable method
- rden2.m - RMS error for real dual-tree method
- cden2.m - RMS error for cmplx dual-tree method
- den3.m - Compare three methods
- soft.m - Soft thresholding



